Photoelectric effect
Physical Background
To study photoeletric effect we can choose one of these methods:
- Method of charging capacitance on stopping voltage – simplier method.
- Study of volt-amperove characteristics of vacuum phototube – more complex method, suitable for university stundets and students of technical subjects.
A. Method of charging capacitance on stopping voltage
In this experiment we study photoelectric effect by method of charging capacitance on stopping voltage U0(f). Outer photoeffect, i.e. freeing electrons from photocatode surface fotokatody by light, happens only and if only the light frequency f is higher than the threshold frequency (also minimum frequency) fm
| f > fm . | (3) |
Electron, which was stamped from the photocatode, reaches the anode, if the electron has sufficient kinetic energy Ek,max. = mev2/2, since it has to overcome repulsive electrostatic force. Electric voltage U responds to work We of electric forces to move unity electric charge Q in electric field (U = We/Q), then we can determine maximal kinetic energy of electrons Ek,max. from measured stopping voltage U0 from relation
| Ek,max. = e·U0 , | (4) |
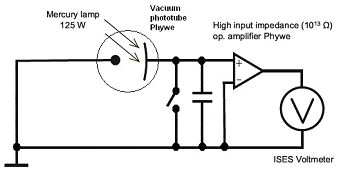
|
| Fig. 1: Diagram of vacuum phototube, with parallelly connected capacitor and switch for dicharge. Photocatode is connected to positive input of operational amplifier, anode to negative input. |
Considering conservation law of energy, A. Einstein explained all observable properties of photoeffect. Using the Planck relation between energy of photon Ef impacting on photocatode
| Ef = h·f , | (5) |
- work needed to emit the electron from the material of photocatode – so called work function Wv
- and the rest of energy to the kinetic energy of electron ... Ek = e·U0.
Einstein equation for outer photoeffect expressed the energy conservation law
| Ef = Wv + Ek , / −Wv | (6) |
| Ek = eU0 = Ef − Wv = h·f − h·fm . | (7) |
We see that mysterious threshold frequency fm is related to work function
| Wv = h·fm | (8) |
Einstein's explanation of photoeffect, which is based on interaction of photon with another particle (here electron), helped later to formulate wave–particle nature of light, which stood at the birth of the quantum mechanics.
Now you can proceed to study chosen method.
B. Study of volt-amperove characteristics of vacuum phototube
where e = 1,602.10−19 C is the charge of electron in the absolute value. Two convenient units for Ek are used: a joule (J), or an electronvolt (eV) where the value corresponds to the absolute value of the stopping voltage in volts.
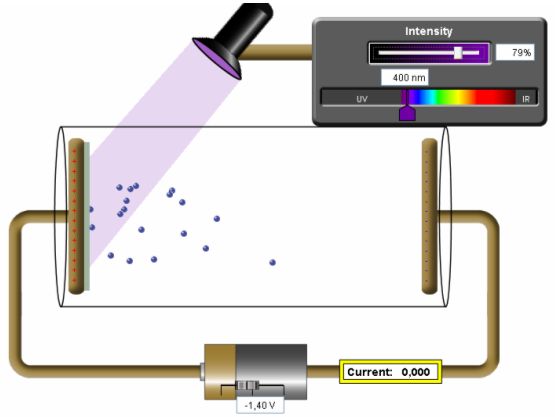
Fig. 1: Visualisation of the photoelectric effect with an applet (http://PhET.colorado.edu). Electrons emitted (kicked out) from the photocathode by the incident violet light (400 nm) are blocked by the negative voltage (stopping voltage −1,40 V) on the anode so that they cannot reach the anode and no current is measured.
We can change the voltage between the cathode and the anode using an external voltage source to study the volt-ampere characteristics of the vacuum phototube. The physical background and the stopping voltage method described above can be visualised and explained with the usage of PhET applet ‘Photoelectric effect’ (see the Fig. 1), accessible for free at
requiring only the JAVA Runtime Environment (JRE) installed on your computer.
There were several interesting characteristics observed with the photocurrent:
- The greater light intensity is incident, the higher photocurrent is measured (as expected).
- The stopping voltage does not depend on the light intensity (surprising).
- The stopping voltage depends on the frequency of the incident electromagnetic radiation (simple dependence U0 = U0(f) = U0(1/λ) was surprising – see the Fig. 2a).
- No photocurrent can be observed for frequencies less than one certain threshold frequency f0 (wavelengths greater than the corresponding threshold wavelength λ0), determined by the material of the photocathode, and regardless of the light intensity (surprising).
- Saturation of the photocurrent occurs for higher positive voltages on the anode. The saturation photocurrent is determined by the intensity of light. (See the Fig. 2b.)
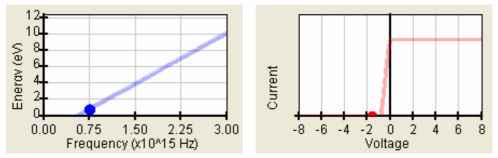
Fig. 2: a) simple dependence kinetic energy of electrons vs. frequency of incident elmg. radiation, b) typical V-A characteristics with the zero photocurrent for U < U0 and the saturation of photocurrent (the photocurrent does not change for higher positive voltages).
The wavelength λ (the threshold wavelength λ0) corresponds to the frequency f (the threshold frequency f0)
where c = 3.108 m/s is the vacuum light velocity. The characteristics II–IV were difficult to explain easily but the experimental dependence Ek(f) = eU0(f) was simply a linear function of the frequency f>f0
where K is the coefficient or the slope as well (see the figure 3).
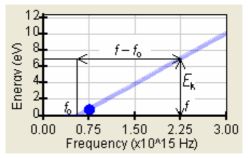
Fig. 3: Observed simple dependence electron energy vs. frequency – linear function (3).
All the characteristics II–IV and the experimental dependence (3) were explained by Albert Einstein at once in 1905 when A. Einstein used the Max Planck’s quantum hypothesis that light is represented by quanta (particles, named photons since 1926) with the energy Ephoton = hf where h = 6,63.10−34 J.s is the Planck constant. Then for K = h we can explain the dependence (3) as the law of conservation of energy
therefore the energy of a photon incident onto the photocathode
is transformed to the work function W = h.f0 necessary to kick the electron out of the photocathode and the rest is equal to the kinetic energy Ek of the electron. Thus, the threshold frequency is related to the work function that is determined by material of the photocathode.
In this explanation we consider interaction between two particles (a photon with sufficient energy and an electron, not an electromagnetic wave with a particle) where the energy-conservation law remains valid.
