Natural and driven oscillations
Physical Background
Harmonic Oscillator
A body making an oscillatory harmonic motion is called the harmonic oscillator. At the first approximation it may be e.g. a body suspended on a spring (Fig. 1) or an atom or a molecule of a solid.
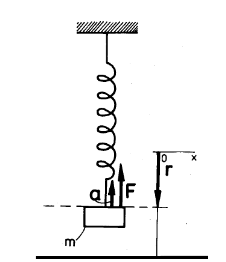
Figure 1 The schematic representation of the harmonic oscillator; F is the elastic force, r is the deflection, a is the acceleration
If the damping resistance of the environment may be neglected, we speak about the undamped harmonic oscillator. We can demonstrate that the oscillation is harmonic, if the acting force is proportional to the deflection from the equilibrium, and its direction is opposite to that of the deflection.
Let us have a spring, for the deflection of which from the equilibrium position by r is necessary to exert the force F = -kr, where k is the spring stiffness. An equation of the motion of the harmonic oscillator, consisting of the spring and the weight with the mass m, is −kr = ma (as the application of the second Newton΄s law Σ F = ma), i.e.


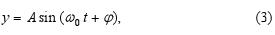
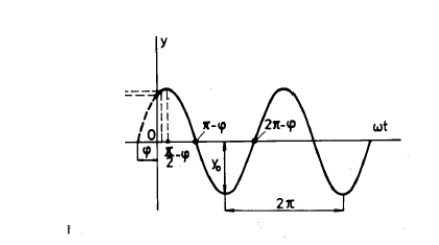
Figure 2. Graphical representation of the harmonic motion
We can write for the natural angular frequency of the undamped harmonic oscillator
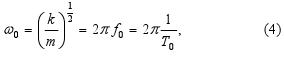
Damped oscillator
During the motion of a harmonic oscillator under real-world conditions friction forces are always acting decreasing the amplitude of the oscillating motion, leading to the standstill after some time. This kind of oscillations is then referred to as a damped oscillator.
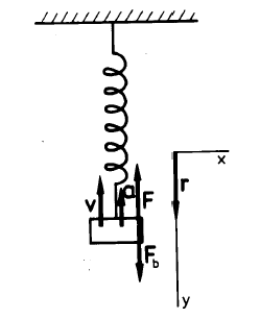
Figure 3 The schematical representation of the damped oscillator;
F is the elastic force, Fb is the damping force, r is the deflection v is the velocity and a is the acceleration
The friction force at low velocities is directly proportional to the instantaneous velocity v of the weight
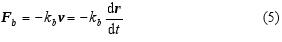

Let us denote the quantity b = kb/(2m), referred to as the damping, [b] = s−1. For a small damping (b < ωo) equation (5) has a solution for r = yj
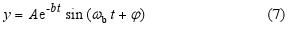
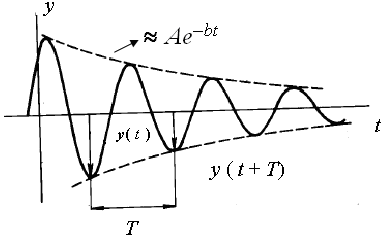
Figure 4 Graphical representation of the damped oscillator
Driven oscillator
The important case of the ocillating motion is the driven oscillator, where an external force makes a material object to oscillate at a generally different frequency, than that of the natural frequency of the oscillator. If, however, both frequencies are approaching each other, the important phenomenon arises, known as the resonance.
Let us assume the weight in Fig. 3 is acted upon by a driving periodic force

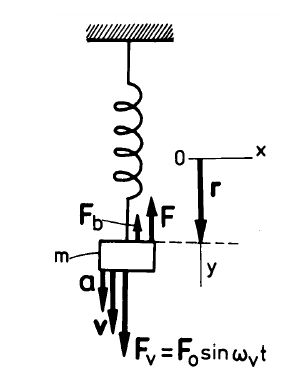
Figure 5 The schematic representation of the driven oscillator;
the driving force Fv, the elastic force F, the damping force Fb, v is the velocity and a is the acceleration
If all the forces that make the weight to move are considered, the following equation of the motion may be written
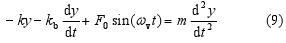
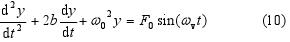

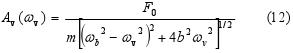
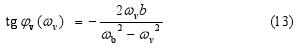
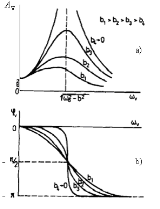
Figure 6 Graphical representation of the driven oscillations on the driving force frequency ωv. with the damping b as the parameter; - the amplitude Av (part a) and the initial phase φv (part b)
The graphs in Fig. 6 reveal some interesting features of the driven oscillations. First, it is obvious that the amplitude of the driven oscillations Av (see Fig. 6 a) is the function of the angular frequency of the driving force ωv. The maximum amplitude of the driven oscillations occurs for the so called resonance frequency, ωv, res

The dependencies in Fig. 6 will be used to determine the energy transferred to the oscillator. This phenomenon is very important in the Nature and for the technology in general as it represents a selective energy transfer between the transmitter of energy and the oscillator only within a certain interval of frequencies or wavelengths. This is e.g. the basis of selective transfer of telecommunication signals or also an absorption of some wavelength of radiation from the Sun by certain molecules, which otherwise would reach the Earth surface.
The energy transferred per a unit time to the oscillator (or the instantaneous time dependent power ) from the driving source
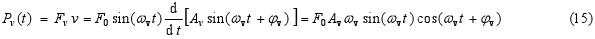
The medium energy transfered in a single period of oscillatory motion from the driving source into the oscillator is then dependent of driving angular frequency ωv (mentioned here without derivation; for more information, see R. B. Lindsay, Physical Mechanics, 3rd ed., Van Nostrand 1962).
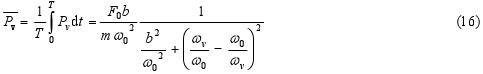
In Fig. 7 is the the medium energy transferred in one period of oscillatory motion to the oscillator from the driving source on the driving angular frequency ωv for various values of damping b.
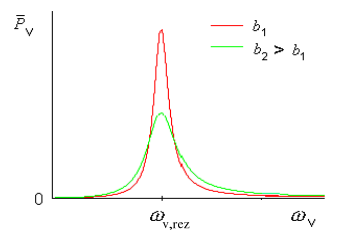
Figure 7 Graphical representation of the medium energy transferred in one period (for two values of damping b)
Author of study text: Prof. Dr. František Schauer, Univerzita Tomáše Bati ve Zlíně
