Spectra
Physical Background
In quantum physics some physical quantities describing objects in microworld (e.g. elementary particles) can't have arbitrary but only some allowed values in contrary to macroworld. In the introduction we mentioned quantization of electron energy in atomic orbital. Quantization effetcs angular momentum of electron, too, and many other quantities.
In 1913, Niels Bohr used these ideas and derived relation for energy and angular momenturm of electronu in hydrogen atom.
Probabilist interpretation of wavefunction can explain us, why are basic physical quantities quantized. Wavefunction is basic tool for description of object properties in microworld. We can't link wavefunction with some visual vlnovou funkci si těžko spojíme s nějakou názornou idea – one reason is it is a complex function. However, its absolute value (which is always real number) is proportional to probability of measuring certain allowed value of physical quantity (e.g. position, momentum, energy, and so on). In simple systems such as hydrogen atoms, the probabilty function should be continuous!
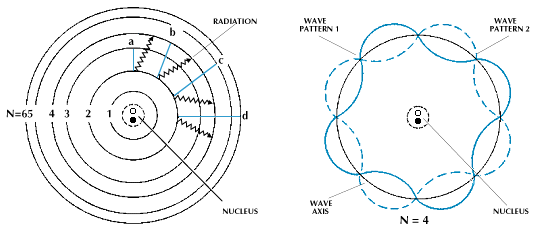
Electron can be described by continuous function, if it is situated on energy level at radius r from the nucleus, which is integer multiple of its wavelength. Using de-Broglie relation for wavelength λB of microworld object, we obtain
![]() ,
,
then the quantization condition is
|
| (1) |
where 2πr is "trajectory length" (circumference), h = 6,63·10−34 J·s is Planck constant, m is mass and v velocity of microworld object and finally n is integer, which is called principal quantum number. From eq. (1) after multiplication by mv/(2π), we get qunatization condition for angular momentum L = rp = rmv
|
| (1a) |
especially we obtain relation for velocity
|
| (1b) |
respectivelly for its square root
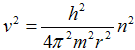 . .
| (1c) |
Velocity v a radius of orbital r are connected trough
action of force. Coulomb attract force 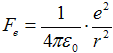 between electron and proton (charge
e = 1,602·10−19 C) caueses centripetal acceleration
between electron and proton (charge
e = 1,602·10−19 C) caueses centripetal acceleration
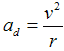 ,
consequently we get
,
consequently we get
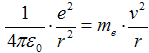 , ,
| (2) |
where me = 9,1·10−31 kg is mass of electron. Kinetic energy is then expressed as
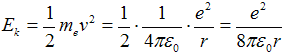 . .
| (2a) |
Substituting from eq. (1c) with squared velocity v2 into eq. (2) can be gained
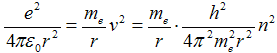 , ,
|
after which we obtain with treatment
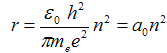 , ,
| (2b) |
where 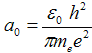 = 5,29·10−11 m is Bohr radius - it is the radius of first orbital (n = 1).
= 5,29·10−11 m is Bohr radius - it is the radius of first orbital (n = 1).
We set potential energy zero in the limit r → ∞. Then dependence of potential energy on radius is
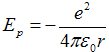 , ,
|
Then total energy from (2a) reads as
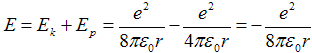 . .
|
After substitution of radius r from (2b) the energy in hydrogen atom is quantized by relation
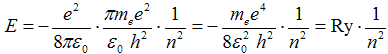 , ,
| (3) |
where the energy of the first state n = 1 is one rydberg and
-1 Ry = -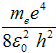 = −13,6 eV . = −13,6 eV .
|
Creation of spectral lines is then easily explained by transitions between energy states, let's denote them with principal quantum numbers m and n (m > n, so En > Em). When electron transitions from higher energy state to lower energy state, photon is emited, having energy
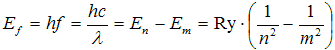 . .
| (4) |
From there it is obtained the relation for wavelength on Rytz-Rydberg combination principle
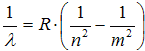 , ,
| (5) |
where ![]() 1,0974·107 m-1 is Rydbergovu constant.
1,0974·107 m-1 is Rydbergovu constant.
For wavelengths from Balmer series of hydrogen spectral lines (electron, which fall to second energy state, n = 2, m > 2) the formulae (5) is exact. The lower is the energy difference between two energy level, the more probable is the transition between these states with emission of a photon. That's reason why transitions between two neighbouring levels are the brightest lines in the spectrum and the intensity of spectral lines in one serie gradually decreases!
