Heisenberg uncertainty principle
Physical Background
Heisenberg uncertainty principle states that the location and momentum of one arbitrary particle cannot be determined simultaneously with infinite accuracy. Let us consider a photon with the mass m and the momentum p. If we measure its position with uncertainty Δy and simultaneously its momentum in the same direction with uncertainty Δpy, then according to Heisenberg uncertainty principle it should be valid

We will carry out the experimental verification of the validity of Heisenberg principle by passing photons through the slit, where photons from the laser (Fig.1) strike perpendicularly slit the screen with the slit of the width d (in the direction of x axis). Their momentum vector p with components px= mc and py = 0, where m is the mass of proton and c = 3,00·108 ms-1 is the velocity of light.
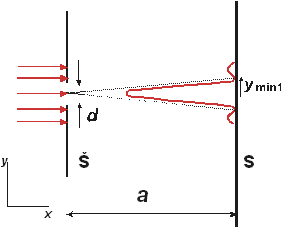
Figure 1 The geometry of the diffraction phenomenon on the slit (Š – slit, S – screen)
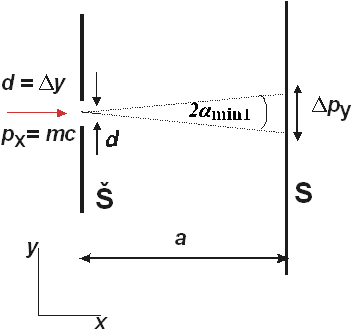
Figure 2 The momentum of photon during the diffraction on the slit (Š – slit, S – screen)
The transfer of a photon throught the slit of width d is, as a matter of fact, the measurement of its position in the direction of y axis, with the result given by the position of the slit y with the uncertainty Δy = d It is indeed true, because the photons that have passed through the slit, and are already behind the screen, should have, at certain moment position y ± d/2. Therefore, we can write for the uncertainty of the position of the photon
Let us examine the momentum p of the photon behind the slit. While the photon in front of the slit that is moving perpendicularly towards the slit, has the momentum px = mc, py= 0, i.e. only in the direction of x axis (Fig. 2), the photon behind the screen has the momentum in the direction of y axis as well, and that is py (Fig.2). We will take the position of the first minimum with respect to the maximum of the diffraction patter as the uncertainty of the photon momentum in the direction of y axis, or (Fig. 2)
What is the magnitude of the corresponding angle αmin1? A photon is a particle with the mass m and the momentum p. From the wave properties of photons is for example, according to the de Broglie relation its wavelength is inversely proportional to the magnitude of its momentum p

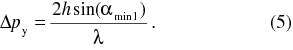
With the use of geometry in the Fig. 2 it is
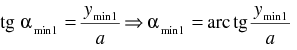
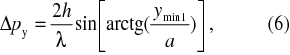
If we multiply both uncertainties in equations (2) and (6) and suppose the validity of the Heisenberg uncertainty principle formulated in equation (1) we have the inequality
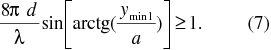
So, if Heisenberg uncertainty principle is valid for photons, the inequality (7) must be valid. We can verify this by the substituting the value of d , and from the value of the position of the first minimum ymin 1. We can proceed also in a different way. On the basis of the measurements and given magnitudes, thanks to equations (2) Δy and (6) Δpy and afterwards with help of the equation (1), we will find out an approximate value of one of the most basic physical constants - Planck constant, of which existence proves the validity of Heisenberg uncertainty principle.
Author of study text: Prof. Dr. František Schauer, Univerzita Tomáše Bati ve Zlíně
