Difraction on microobjects
Experiment
As a source of a monochromatic and coherent radiation we will use two lasers of the wavelengths λ1 = (632 ± 10) nm and λ2 = (532 ± 10) nm. Their radiation falls on a slit. The distribution of the intensity of laser radiation behind the slit, in a diffraction pattern, is picked up using a semiconductor photodiode situated at a distance of a = (2152 ± 1) mm from the slit (see Fig. 3) and amplifiers of the system ISES. A XY recorder is attached to it allowing to scan the distribution of the intensity of the diffraction pattern. A schematic arrangement of the experiment is in Fig. 3.
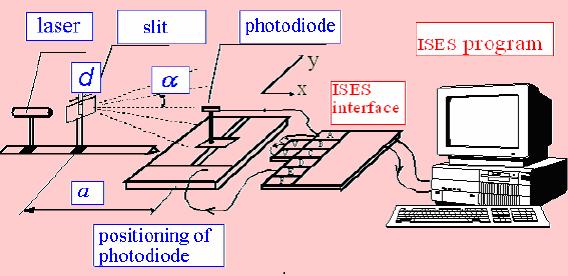
Figure 3 The arrangement of the diffraction experiment on the slit scanned by ISES system and transmitted by the Internet.
The signal from an optical module is connected to the data transmission channel A of a unit ISES,. The XY recorder is fed to the output channel E of ISES and ensures the scan of the photodiode. For the maximum precision of the measurement of the dimension of the microobjects it is necessary to take a signal from the main maximum and at least from another two maxima. The detailed knowledge of the intensity distribution of the diffraction can be used to find the size of a microobject - in our case, to find the width of the slit.
This can be done either by using the equation (1) or using a knowledge of locations of minima, or maxima and equations (3) or (4). In the Fig. 4, there is an example of the measured data with the fitted function (1) carried out by the program Origin 7.5. The difference in the accuracy of the determination of the slit size using both methods is substantial.
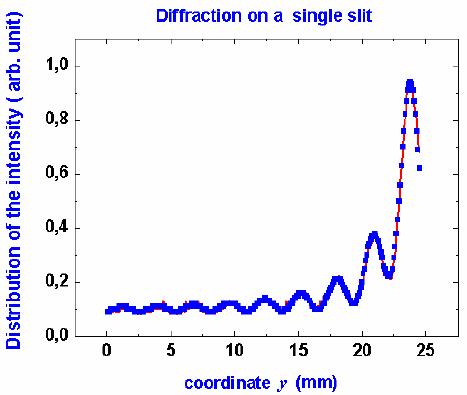
Figure 4 An example of the distribution of light intensity of the diffraction on the single slit; laser of λ1 = 628,10 nm (d = 180 μm), the with determined by the single maximum position gives d = (170 ± 10) μm, the red curve gives the fit by the optimalisation programme d = (168.6 ± 0.4) μm.
- Look at the page, all interactive features of experiment, and all you see. Can you imagine the experiment having your eyes closed?
- Before full-fledged measurement, do one arbitrary measurement. Before next measurement, try to predict, how changes of some physical wuantity will change other quantities. Have you figured out, that you can download mesured data to computer?
