iSES - Internet School Experimental System

 

Home News Remote Laboratory System iSES Contacts

Electromagnetic induction

Physical Background

Electromagnetic induction is the phenomenon of the mutual coupling of the magnetic and electric fields, where the electric field is generated whenever a time varying magnetic field is present. For example, in the introductory experiment in the picture above there is a bar magnet moving in the direction of the winding and thus creating the time dependent magnetic field. We can observe the deviation on the connected measuring instrument. This deviation is caused by the time dependent electric field in the coil. This phenomenon is called electromagnetic induction. Electromagnetic induction is used for example in dynamos or alternators, which are the devices for transforming mechanical energy into electrical one.

For the quantitative description of the experiment we need to introduce a few physical quantities and symbols.

Magnetic flux through the area of the winding

If for any point of the plane limited by the winding of the area S, B = const. is fulfilled, then the magnetic flux is defined as

where Φ_mag is the magnetic flux, [Φ_mag] = Wb, weber; B is a magnetic induction [B] = T, tesla; dS is the element of the area, and α is the angle between vectors B and dS. Electromotive force ε, [ε] = V, volt, induced in one winding is described by Faraday´s law of electromagnetic induction: The magnetic flux may change due to:

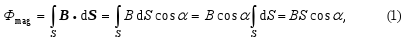
• the change of the magnitude of the magnetic induction B(t) with time,
• the change of the dimension of the surface S(t),
• the change of a mutual orientation of vectors B and dS, α(t).

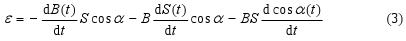
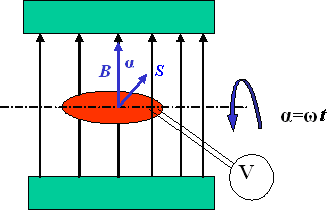
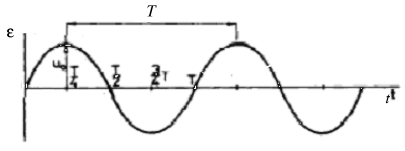
We will use in our experiment the third component (rotating coil in the homogeneous magnetic field, Fig. 2). In this particular experiment we will use the arrangement from the Fig. 2 in which a flat coil of area S rotates around the fixed axis, which lies in the coil plane, in a homogeneous magnetic field with the magnetic induction B.
The electromotive voltage induced in one winding is, according to the equation (3), (considering the time independence B(t) = const. and S(t) = constant) Because the coil rotates with the constant angular frequency ω = 2π/T , where T denotes the period of revolutions, then we may write for the angle α, α = ωt, (see picture 2, graph of dependence (5) and calculation (6) ). Then, for a coil with N windings we have Integrating the previous equation (5) we have an important condition that should be fulfilled if the Faraday s law is valid.

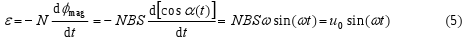
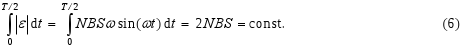
Author of study text: Prof. Dr. František Schauer, Univerzita Tomáše Bati ve Zlíně

---