iSES - Internet School Experimental System: Remote Laboratory

Remote Experiments

Radioactivity (5 experiments)

Physical Background

In remote experiment we will observe statistical laws, ie. dependency of measured values on measuring time, respectively count of repeated measurements, dependency of radioactive measure on variable conditions, that is: distance from radioactive emitter, thickness of shielding material, type of shield. Radioactive measure is defined by count of events, which are detected by Geiger-Müller detector.

Subtasks:

Meaning of statistical treatment – common for all tasks.

Natural background – studium of natural radioactive background with possibility to check validity of Poisson distribution for rare phenomenon.
Protection with distance – basic intuitive way of protection against radioactivity together with minimalization doby expozice.
Protection with shielding – standard way of protection against ionizing radiation used in indusry and health care.

I. Significance of statistical treatment

Statistics as instrument to describe and predict random event

Random or stochastic phenomenon, eg. radioactive decay of unstable nucleus and related ionizing radiation, is unable to be predicted, when it happens (on contrary from position of planets etc). However, it is possible to measure and predict measure of occurence, in other words frequency of phenomenon by repeated mesurement in longer time. For selected measurement time it has sense to repeat measurements and statistically evaluate results using:

Arithmetic mean n_p – defines searched measure of radioactivity. its value is the most probable value to measure from N repeated measurements. We can say that there exists a typical (average, most probable) value, to which arithmetic mean will converge with increasing number of repeated measurements. For small count of repeated measurements there is very low garancy that we get typical value. Thus it is desirable to realize many measurements.
Corrected sample standard deviation – says how big is uncertainty of experiment, how much the arithmetic mean deviates from real value for given conditons. Increasng number of measurements will increase precision in given conditions, so corrected sample standard deviation (measure of uncertainty) will decrease.

A. Natural radioactive background – validation of Poisson distribution

In first task we will measure value of natural radioactive background B. As a result we will obtain arithmetic mean B_p (from english background) out of selected number of repetitions of measurements and corrected sample standard deviation σ_B as an error of our measurement. Result will be written in form

B = B_p ± σ_B (that is: result = arithmetic mean ± uncertainty of experiment).

We can verify law for low probable phenomenon, which is described by Poisson distribution. When repeating measurement, which lasts fixed amount of time (eg. 1 minute), we detect various number of detections B_i 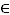[0;B_max], and every value from this values n_i–times (repetitions). These tzv. frequencies areproportional to probabilities p_i of measuring given number of detections (so values B_i are measured with frequency n_i). For probabilities p_i it is possible to verify Poisson distribution, which theoreticly predicts those values of probability of less probable phenomenon.

Eg. in office software MS Excel we can use statistical functions AVERAGE, STDEV and POISSON.

Important notice for other tasks

When studying phycial laws valid for protection against ionizing raditation (distance, material thickness and material type), it is crucial to realize that all measured data will contain contribution from natural radioactive background. The intensity of radioactive background can be measured by second Geiger-Müller detector. This data can be substracted from main measurement (when both measurements are done at the same time) or it is possible to mesure natural radioactive background afterwards, calculate average, which is then substracted from main measurement.

So we will examine number of pulses minus number of pulses from natural radioactive background in remaining experiments and its dependency on distance from radiation emitter or on material thickness and type. During experiment we will measire several points of physical dependences. Meanwhile we can learn about importance of statistical processing and about choice of number of repetitions (alias dependence on choice of statistical set size). It is not appropriate to use only one measured value for each point of examined dependence. Measurement should be few times repeated in every point and therefore we can use average number of pulses and corrected sample standard deviation as measurement uncertainty in every point. Meanwhile values from only one measurement are widely dispersed around expected dependence, average values from several repetitions are less dispersed and will have higher reliability using statistical errors. Our remote experiment measures continuously and repetatedly and allows to choose desired data so they can be statistically processed. Statistical data will from almost continous dependece for so large statistical set and they can be well compared with theoretical dependence.

B. Protection with distance from radiactive emitter

Ionizing radiation (as light and other types of radiation) has to fulfill basic dependency describing decrease of intensity with increasing distance. For point emitter the radiation intensity decreases as r ^-2 (minus second power of distance), because surface of sphere in given space angle increases as r² (second power of sphere radius).

Fig. 1: Illustration to inverse square law – decrease of intensity with squared distance. Since effective detector area is constant and emitter emits radiation uniformly in all directions, in double (and far enough) distance from emitter we measure four-times less number of pulses, as the appropriate space angle (showed in blue lines) will be four-times smaller.

In far eoungh distance it is possible to neglect difference between spherical surface and effective detector area. Also the emitter can be in far distances considered as point. However, in close distance it is necessary to calculate with geometry of experiment and dependence becomes much more complicated.

C. Protection with shielding

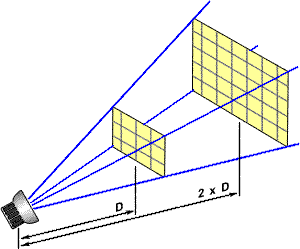
Consider ionizing radiation which comes through layer of some material, some part of entering intensity can be absorbed so it doesn't leave the material. So we measure less intensity, less number of pulses behind the material. Let's find correct theoretical dependence of number of detected pulses on material thickness. Let's split the material (considered to be homogenous) on several layers, which have same width and are identical. We can suppose that every layer decreases entering intensity with same ration, that is radtiation exits every layer β-times smaller, where β= I₁/I₀ = I₂/I₁ = I₃/I₂ = … = I_N/I_N−1 < 1 (see fig. 2). This results in following relations

I₁ = β I₀ , I₂ = β I₁ = β·β·I₀ = β²I₀ , I₃ = β I₂ = β³I₀ , … I_N = β I_{N − 1} = β^NI₀ .

(1)

Fig. 2: Derivation of Lambert–Beer law.

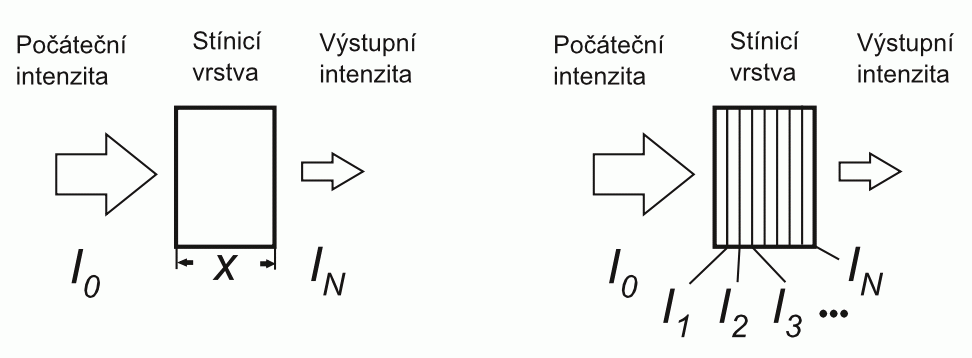
Ratio β depends on material type and on choice mentioned layers. Let's replace this parameter with appropriate material characteristics, which uses Euler number e = 2,71828… (it is the base of natural exponential function). We can assume that number of layers N is proportional to whole width of shielding material x, so N = k·x. Using relation β = e^{ln β} we get relation for decreased intensity

I_N = β^NI₀ = (e^{ln β})^NI₀ = (e^{ln β})^kxI₀ = I₀ e^{ln β kx} = I₀ e^−Cx ,

(1)

where C = −lnβ·k is so called linear decrease coefficient (decrease of intensity determines the minus sign). Cefficient C (unit m⁻¹) says which material width decreases the incoming intensity e-times.

We have just discovered number of pulses of ionizing radiation N(x) minus number of pulses from natural radioactive background B (so it is N(x) − B), which is measured behind the material of thickness x, depending on this thickness. This function decreases exponentially.

(1)

Here A is constant proportional to activity of ionizing source emitter and C is linear decrease coefficient. Coefficient C depends on shielding material density, material (proton number) and energy of ionizing radiation. In technology it is useful to mention absorption half-width, which is the width of material where intensity is half decreased. In following table you can find some half-widths for water, concrete, iron (Fe) and lead (Pb) for gamma radiation at energies from 200 keV to 5000 keV.

Half-width [mm]

E [keV]	water	concrete	iron (Fe)	lead (Pb)
200	51	21	6,6	1,4
500	78	30	11,1	4,2
1000	102	45	15,6	9
2000	144	59	21	13,5
5000	231	99	28,8	14,7

Tab. 1: Half-widths for water, concrete, iron and lead for various energies of gamma radiation (taken from Ullmann V.: Jaderná fyzika a fyzika ionizujícího záření).