Heisenbergův princip neurčitosti
Physical Background
Heisenbergův princip neurčitosti stanovuje, že lokalizace polohy a hybnosti libovolné částice nemůže být současně s nekonečnou přesností. Vezměme foton hmotnosti m a hybnosti p. Pokud měříme polohu fotonu s odchylkou Δy a současně jeho hybnost ve směru pohybu fotonu s odchylkou Δpy, potom podle Heisenbergova principu by mělo platit

Ověřme Heisenbergův princip pomocí fotonu nacházejícího se v paprsku světla vycházejícího z laseru, který prochází štěrbinou šířky d kolmo na rovinu štěrbiny a též kolmo na stínítko nacházející se ve vzdálenosti a od štěrbiny (obr. 1). V námi uvažovaném případě vektor hybnosti fotonu p má složky px= mc a py = 0, kde m je hmotnost fotonu a c = 3,00·108 ms-1 je rychlost světla (obr. 2).
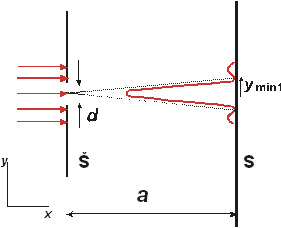
Obr.1 Geometrie experimentu difrakce na štěrbině (Š – štěrbina, S – stínítko)
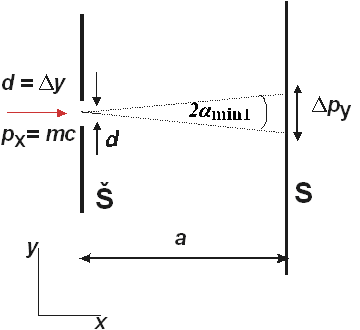
Obr. 2 Hybnost fotonu při ohybu na štěrbině (Š – štěrbina, S – stínítko)
Průchod fotonu skrz štěrbinu šířky d je vlastně měření jeho polohy ve směru osy y, s výsledkem určení polohy y s odchylkou Δy = d. Což je skutečně pravda, protože fotony, které proletěly štěrbinou a nacházejí se už za ní na stínidle, by měly mít v určitém okamžiku polohu y ± d/2. Proto můžeme napsat pro odchylku polohy fotonu
Prozkoumáme vektor hybnosti p fotonu za štěrbinou. Pokud foton před štěrbinou, pohybující se kolmým směrem ke štěrbině má složky vektoru hybnosti px = mc, py = 0, t.j.. jen ve směru osy x (obr. 2), foton za štěrbinou má i složku hybnosti ve směru osy y, kterou označíme py. Dostaneme polohu prvního minima vzhledem k poloze hlavního difrakčního maxima jako odchylku momentu hybnosti fotonu ve směru y-osy (obr. 2)
Jaká je velikost odpovídajícího úhlu αmin1? Foton je částice s hmotností m a hybností p. Z vlnových vlastností fotonu na základě de Broglieho vztahu pro vlnovou délku vyplývá, že vlnová délka λ je nepřímo úměrná velikosti vektoru hybnosti p

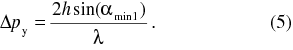
Na základě geometrie z obr. 2 platí
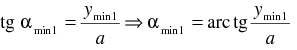
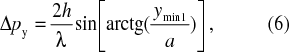
Pokud vynásobíme odchylky v rovnici (2) a (6) a předpokládáme platnost Heisenbergova principu neurčitosti, formulovaného vztahem (1), dostáváme nerovnost
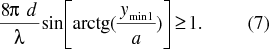
Na základě našich měření, daných hodnot a pomocí vztahů (2) pro Δy a (6) pro Δpy , s následným využitím vztahu (1), lze najít přibližnou hodnotu h, hodnotu jedné ze základních fyzikálních konstant h – Planckovy konstanty, která potvrzuje platnost Heisenbergova principu neurčitosti.
Autor studijního textu: Prof. Dr. František Schauer, Univerzita Tomáše Bati ve Zlíně
